선형결합된 확률변수의 적률생성함수는 어떤 모양을 가질까?

○ 선형결합된 확률변수의 적률생성함수(Moment Generating Function, mgf)

○ $Y\, =\,  \sum_{i=1}^{n}X_{i}$(x의 합),  $\overline{X}\, =\,  \frac{1}{n}\sum_{i=1}^{n}X_{i}$(x의 평균)의 적률생성함수(Moment Generating Function, mgf)

 

○ 예제 1) 베르누이분포 선형결합 → 이항분포의 적률생성함수

○ 예제 2) 지수분포 선형결합 → 감마분포의 적률생성함수

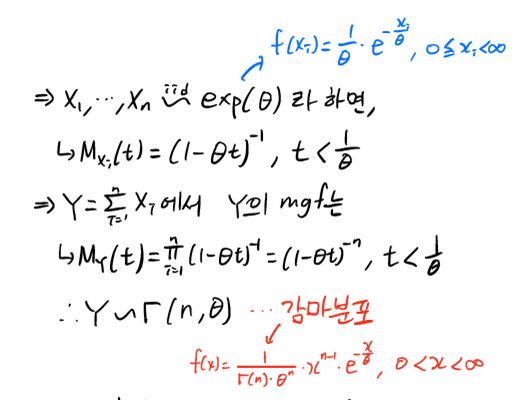
○ 예제 3) 카이제곱분포의 적률생성함수

○ 예제 4) 표준정규분포에서의 적률생성함수