문제 15번
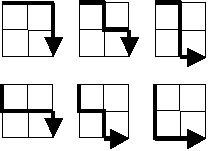
아래와 같은 2 × 2 격자의 왼쪽 위 모서리에서 출발하여 오른쪽 아래 모서리까지 도달하는 길은 모두 6가지가 있습니다 (거슬러 가지는 않기로 합니다).
그러면 20 × 20 격자에는 모두 몇 개의 경로가 있습니까?
접근방법(1차) - 코드는 맨 밑에!

1. 중고등학생 때 시험문제로 종종 나왔던 문제라, 접근방법 찾는 것은 그리 어렵지 않다.(순열 문제임)
(1X1) 격자의 경우 2, (2X2) 격자의 경우 6, (3X3) 격자의 경우 20, 이런 방식으로 구하면 된다.

2. 대각선으로 나열된 것을 가로로 배치해보면

3. 위와 같은 형태가 되고, 우리는 40C20 (콤비네이션 / 컴비네이션)을 구하면 된다.
4. 가장 먼저 생각해 볼 수 있는 것은 재귀함수이다. nCr = (n-1)C(r-1) + (n-1)Cr 을 이용하면 된다.
→ 거꾸로 거슬러 올라가는 것을 반복하는 구조라, 숫자가 커서 시간이 너무 오래 걸린다.

접근방법(2차)
1. 재귀함수를 계속 반복하는 형태가 아닌, 위에서 아래로 한단계 내려갈 때만 사용하도록 변경한다.
2. 이중 포인터를 이용해 동적할당 함수를 만든 다음, (21X11)크기의 2차원 배열을 선언해 준다.
→ func(20 , 10) 으로 직관적으로 바로 산출하기 위해 +1 크기의 배열을 선언!


접근방법(2차) 코드
#include <iostream>
using namespace std;
long long comb(const int n, const int r)
{
long long** comb_array = new long long* [n + 1];
for (int i = 0; i < n + 1; i++)
{
comb_array[i] = new long long[r + 1] ;
}
for (int m = 0; m < n+1; m++)
{
for (int q = 0; q < r+1; q++)
{
if (q > m)
{
comb_array[m][q] = 0;
}
else if (m == q || q == 0)
{
comb_array[m][q] = 1;
}
else
{
comb_array[m][q] = comb_array[m - 1][q - 1] + comb_array[m - 1][q];
}
//cout << comb_array[m][q] << " ";
}
//cout << endl;
}
return comb_array[n][r];
}
int main()
{
cout << "Answer is : " << comb(40, 20) << endl;
return 0;
}
접근방법(1차) 코드
#include <iostream>
using namespace std;
long long comb(int n, int r)
{
if (n == r || r == 0)
return 1;
else
return comb(n - 1, r - 1) + comb(n - 1, r);
}
int main()
{
cout << "Answer is : " << comb(40, 20) << endl;
return 0;
}
참고
https://github.com/mannlim/ProjectEuler
mannlim/ProjectEuler
How to solve Project Euler using by C++. Contribute to mannlim/ProjectEuler development by creating an account on GitHub.
github.com
'알고리즘 문제 & 프로그래밍 > C++' 카테고리의 다른 글
| [C++]프로젝트 오일러 17번 문제&풀이 (1부터 1000까지 영어로 썼을 때 사용된 글자의 개수는?) (0) | 2020.11.26 |
|---|---|
| [C++]프로젝트 오일러 16번 문제&풀이 (2의 1000승의 각 자릿수를 모두 더하면?) (0) | 2020.11.25 |
| [C++]프로젝트 오일러 14번 문제&풀이 (백만 이하로 시작하는 우박수 중 가장 긴 과정을 거치는 것은?) (0) | 2020.11.24 |
| [C++]프로젝트 오일러 13번 문제&풀이 (50자리 수 100개를 더한 값의 첫 10자리 구하기) (0) | 2020.11.24 |
| [C++]프로젝트 오일러 12번 문제&풀이 (500개 이상의 약수를 갖는 가장 작은 삼각수는?) (0) | 2020.11.23 |




댓글