반응형
문제
양의 정수 n에 대하여, 다음과 같은 계산 과정을 반복하기로 합니다.
n → n / 2 (n이 짝수일 때)
n → 3 n + 1 (n이 홀수일 때)
13에 대하여 위의 규칙을 적용해보면 아래처럼 10번의 과정을 통해 1이 됩니다.
13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
아직 증명은 되지 않았지만, 이런 과정을 거치면 어떤 수로 시작해도 마지막에는 1로 끝나리라 생각됩니다.
(역주: 이것은 콜라츠 추측 Collatz Conjecture이라고 하며, 이런 수들을 우박수 hailstone sequence라 부르기도 합니다)
그러면, 백만(1,000,000) 이하의 수로 시작했을 때 1까지 도달하는데 가장 긴 과정을 거치는 수는 얼마입니까?
참고: 계산 과정에는 백만을 넘어가는 수가 나와도 괜찮습니다.
접근방법
1. 벡터를 2개 생성한다. 하나는 숫자를 담는 벡터(num_vec), 다른 벡터(count_vec)는 과정의 갯수(count)이다.
2. 과정의 갯수가 담겨 있는 벡터(count_vec) 안에서 가장 큰 값을 구한다.(max_value)
3. 가장 큰 값이 나온 자리에 위치한 숫자가 담겨있는 벡터(num_vec)의 값을 산출하면 끝!
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
long long i = 1;
int max_value = 0;
vector<long long> num_vec;
num_vec.clear();
vector<int> count_vec;
count_vec.clear();
while (i <= 1000000)
{
long long j = i;
int count = 0;
while (true)
{
if (j == 1)
break;
else if (j % 2 == 0)
{
j = j / 2;
}
else
{
j = 3 * j + 1;
}
count++;
}
cout << i << " : " << count << endl;
num_vec.push_back(i);
count_vec.push_back(count);
max_value = max(max_value, count_vec[i-1]);
i++;
}
int l = 0;
while (true)
{
if (count_vec[l] == max_value)
break;
l++;
}
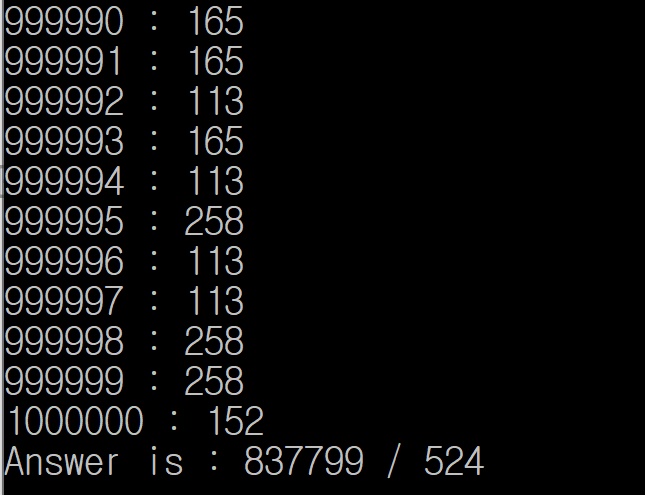
cout << "Answer is : " << num_vec[l] << " / " << count_vec[l] << endl;
return 0;
}
참고
https://github.com/mannlim/ProjectEuler
mannlim/ProjectEuler
How to solve Project Euler using by C++. Contribute to mannlim/ProjectEuler development by creating an account on GitHub.
github.com
반응형
'알고리즘 문제 & 프로그래밍 > C++' 카테고리의 다른 글
| [C++]프로젝트 오일러 16번 문제&풀이 (2의 1000승의 각 자릿수를 모두 더하면?) (0) | 2020.11.25 |
|---|---|
| [C++]프로젝트 오일러 15번 문제&풀이 (20×20 격자의 좌상단에서 우하단으로 가는 경로의 수) (0) | 2020.11.25 |
| [C++]프로젝트 오일러 13번 문제&풀이 (50자리 수 100개를 더한 값의 첫 10자리 구하기) (0) | 2020.11.24 |
| [C++]프로젝트 오일러 12번 문제&풀이 (500개 이상의 약수를 갖는 가장 작은 삼각수는?) (0) | 2020.11.23 |
| [C++]프로젝트 오일러 11번 문제&풀이 (20×20 격자에서 연속된 네 수의 곱 중 최댓값) (0) | 2020.11.22 |




댓글